ساخت هوش مصنوعی ساده با پایتون: قسمت چهارم، ساخت کلاس شبکه عصبی

رضا دهقان

۱ آذر ۱۴۰۲

تکنولوژی ، مقالات

مدت مطالعه: ۵ دقیقه

تعداد بازدید‌: ۵۹۸

هوش مصنوعی

بالاخره نوبت به ساخت کلاس شبکه عصبی رسیده است. اما قبل از آن ما فرایند پس‌انتشار را با به‌روزرسانی بایاس شروع می‌کنیم. ما باید مشتق تابع خطا را نسبت به بایوس حساب کنیم. سپس همین‌طور رو به عقب ادامه داده و با محاسبه مشتق‌های جزیی متغیر bias را پیدا می‌کنیم.

ساخت هوش مصنوعی ساده با پایتون: قسمت سوم، آموزش شبکه‌های عصبی

از آن‌جایی که ما از انتها به ابتدا حرکت می‌کنیم، باید مشتق جزیی خطا نسبت به پیش‌بینی را پیدا کنیم که با متغیر derror_dprediction در تصویر زیر نمایش داده می‌شود:

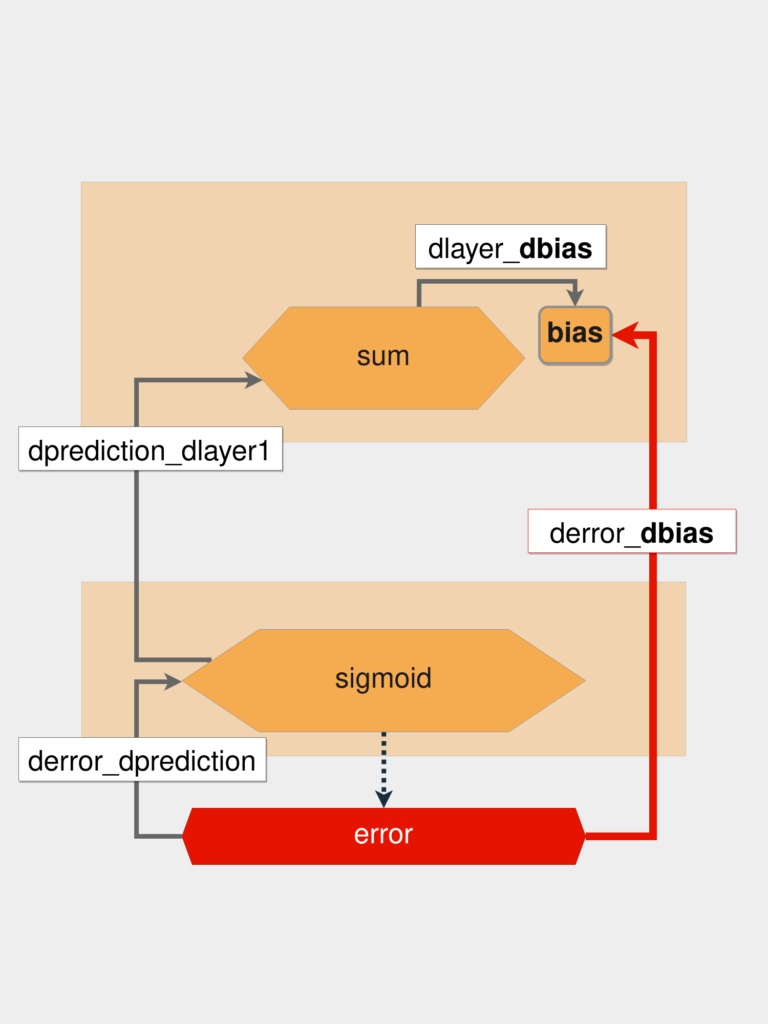
اگر بعد از محاسبه اولین مشتق جزیی (متغیر derror_dprediction) بایاس را پیدا نکردید، باید یک گام دیگر به عقب برگشته و مشتق پیش‌بینی را نسبت به لایه قبلی (متغیر dprediction_dlayer1) محاسبه کنیم.

مقدار پیش‌بینی حاصل تابع سیگموید است و برای محاسبه مشتق آن کافی است مقدار زیر را حساب کنیم:

sigmoid(x)*(1 – sigmoid(x))

حالا کافی است مشتق layer_1 را نسبت به بایاس به دست آوریم. حالا و بعد از چند عملیات مقدار متغیر بایاس را داریم که بعد از اجرای قانون توان برابر با ۱ می‌شود. این فرایند را در قالب کد زیر پیاده‌سازی می‌کنیم:

In &#091;36]: def sigmoid_deriv(x):
  ...:     return sigmoid(x) * (1-sigmoid(x))

In &#091;37]: derror_dprediction = 2 * (prediction - target)
In &#091;38]: layer_1 = np.dot(input_vector, weights_1) + bias
In &#091;39]: dprediction_dlayer1 = sigmoid_deriv(layer_1)
In &#091;40]: dlayer1_dbias = 1

In &#091;41]: derror_dbias = (
  ...:     derror_dprediction * dprediction_dlayer1 * dlayer1_dbias
  ...: )

۱۰

۱۱

In &#۰۹۱;۳۶]: def sigmoid_deriv(x):

...: return sigmoid(x) * (۱-sigmoid(x))

In &#۰۹۱;۳۷]: derror_dprediction = 2 * (prediction - target)

In &#۰۹۱;۳۸]: layer_1 = np.dot(input_vector, weights_1) + bias

In &#۰۹۱;۳۹]: dprediction_dlayer1 = sigmoid_deriv(layer_1)

In &#۰۹۱;۴۰]: dlayer1_dbias = 1

In &#۰۹۱;۴۱]: derror_dbias = (

...: derror_dprediction * dprediction_dlayer1 * dlayer1_dbias

...: )

برای به‌روزرسانی وزن‌ها هم همین فرایند را باید تکرار کنیم. مشتق ضرب داخلی برابر است با ضرب مشتق بردار اول در بردار دوم به‌علاوه ضرب مشتق بردار دوم در بردار اول.

ساخت کلاس شبکه عصبی

حالا که فرایند به‌روزرسانی وزن‌ها و بایاس را فرا گرفتیم، زمان آن رسیده که یک کلاس برای شبکه عصبی بسازیم. وضیفه کلاس NeuralNetwork تولید مقادیر تصادفی اولیه برای وزن‌ها و بایاس است:

class NeuralNetwork:
    # ...

    def train(self, input_vectors, targets, iterations):
        cumulative_errors = &#091;]
        for current_iteration in range(iterations):
            # Pick a data instance at random
            random_data_index = np.random.randint(len(input_vectors))

            input_vector = input_vectors&#091;random_data_index]
            target = targets&#091;random_data_index]

            # Compute the gradients and update the weights
            derror_dbias, derror_dweights = self._compute_gradients(
                input_vector, target
            )

            self._update_parameters(derror_dbias, derror_dweights)

            # Measure the cumulative error for all the instances
            if current_iteration % 100 == 0:
                cumulative_error = 0
                # Loop through all the instances to measure the error
                for data_instance_index in range(len(input_vectors)):
                    data_point = input_vectors&#091;data_instance_index]
                    target = targets&#091;data_instance_index]

                    prediction = self.predict(data_point)
                    error = np.square(prediction - target)

                    cumulative_error = cumulative_error + error
                cumulative_errors.append(cumulative_error)

        return cumulative_errors

۱۰

۱۱

۱۲

۱۳

۱۴

۱۵

۱۶

۱۷

۱۸

۱۹

۲۰

۲۱

۲۲

۲۳

۲۴

۲۵

۲۶

۲۷

۲۸

۲۹

۳۰

۳۱

۳۲

۳۳

۳۴

class NeuralNetwork:

# ...

def train(self, input_vectors, targets, iterations):

cumulative_errors = &#۰۹۱;]

for current_iteration in range(iterations):

# Pick a data instance at random

random_data_index = np.random.randint(len(input_vectors))

input_vector = input_vectors&#۰۹۱;random_data_index]

target = targets&#۰۹۱;random_data_index]

# Compute the gradients and update the weights

derror_dbias, derror_dweights = self._compute_gradients(

input_vector, target

)

self._update_parameters(derror_dbias, derror_dweights)

# Measure the cumulative error for all the instances

if current_iteration % ۱۰۰ == ۰:

cumulative_error = ۰

# Loop through all the instances to measure the error

for data_instance_index in range(len(input_vectors)):

data_point = input_vectors&#۰۹۱;data_instance_index]

target = targets&#۰۹۱;data_instance_index]

prediction = self.predict(data_point)

error = np.square(prediction - target)

cumulative_error = cumulative_error + error

cumulative_errors.append(cumulative_error)

return cumulative_errors

در این چند خط کد اتفاقات زیادی در حال جریان است:

خط ۸: یک نمونه تصادفی از دیتاست انتخاب می‌کند.

خطوط ۱۴ تا ۱۶: متشق‌های جزیی را محاسبه کرده و مشتق بایاس و وزن‌ها را به ما می‌دهد.

خط ۱۸: مقدار بایاس و وزن‌ها را به‌روزرسانی می‌کند.

خط ۲۱: بررسی می‌کند که آیا ایندکس تکرار در ۱۰۰ ضرب شده یا خیر. این کار برای این است که مقدار تغییر خطا بعد از هر ۱۰۰ تکرار را مشاهده کنیم.

خط ۲۴: یک حلقه که تمام تمام نمونه‌های داده را بررسی می‌کند.

خط ۲۸: نتیجه متغیر prediction را محاسبه می‌کند.

خط ۲۹: مقدار متغیر error برای هر نمونه را محاسبه می‌کند.

خط ۳۱: در این خط شما مجموع خطاها را با کمک متغیر cumulative_error حساب می‌کنید.

به طور خلاصه در این کلاس شما یک نمونه تصادفی از دیتاست را انتخاب کرده، گرادیان را محاسبه و وزن‌ها و بایاس را به‌روزرسانی می‌کنید. همچنین شما مجموع خطاها در هر ۱۰۰ تکرار را حساب کرده و از آن برای نمایش میزان تغییر خطا بهره می‌برید.

برای ساده کردن کد، ما از یک دیتاست با ۸ نمونه استفاده می‌کنیم. حالا می‌توانیم تابع ()train را فراخوانی کرده و از کتابخانه Matplotlib برای رسم خطای تجمعی هر نمونه استفاده کنیم:

In &#091;45]: # Paste the NeuralNetwork class code here
  ...: # (and don't forget to add the train method to the class)

In &#091;46]: import matplotlib.pyplot as plt

In &#091;47]: input_vectors = np.array(
  ...:     &#091;
  ...:         &#091;3, 1.5],
  ...:         &#091;2, 1],
  ...:         &#091;4, 1.5],
  ...:         &#091;3, 4],
  ...:         &#091;3.5, 0.5],
  ...:         &#091;2, 0.5],
  ...:         &#091;5.5, 1],
  ...:         &#091;1, 1],
  ...:     ]
  ...: )

In &#091;48]: targets = np.array(&#091;0, 1, 0, 1, 0, 1, 1, 0])

In &#091;49]: learning_rate = 0.1

In &#091;50]: neural_network = NeuralNetwork(learning_rate)

In &#091;51]: training_error = neural_network.train(input_vectors, targets, 10000)

In &#091;52]: plt.plot(training_error)
In &#091;53]: plt.xlabel("Iterations")
In &#091;54]: plt.ylabel("Error for all training instances")
In &#091;54]: plt.savefig("cumulative_error.png")

۱۰

۱۱

۱۲

۱۳

۱۴

۱۵

۱۶

۱۷

۱۸

۱۹

۲۰

۲۱

۲۲

۲۳

۲۴

۲۵

۲۶

۲۷

۲۸

۲۹

۳۰

In &#۰۹۱;۴۵]: # Paste the NeuralNetwork class code here

...: # (and don't forget to add the train method to the class)

In &#۰۹۱;۴۶]: import matplotlib.pyplot as plt

In &#۰۹۱;۴۷]: input_vectors = np.array(

...: &#۰۹۱;

...: &#۰۹۱;۳, ۱.۵],

...: &#۰۹۱;۲, ۱],

...: &#۰۹۱;۴, ۱.۵],

...: &#۰۹۱;۳, ۴],

...: &#۰۹۱;۳.۵, ۰.۵],

...: &#۰۹۱;۲, ۰.۵],

...: &#۰۹۱;۵.۵, ۱],

...: &#۰۹۱;۱, ۱],

...: ]

...: )

In &#۰۹۱;۴۸]: targets = np.array([0, 1, 0, 1, 0, 1, 1, 0])

In &#۰۹۱;۴۹]: learning_rate = 0.1

In &#۰۹۱;۵۰]: neural_network = NeuralNetwork(learning_rate)

In &#۰۹۱;۵۱]: training_error = neural_network.train(input_vectors, targets, 10000)

In &#۰۹۱;۵۲]: plt.plot(training_error)

In &#۰۹۱;۵۳]: plt.xlabel("Iterations")

In &#۰۹۱;۵۴]: plt.ylabel("Error for all training instances")

In &#۰۹۱;۵۴]: plt.savefig("cumulative_error.png")

نمودار زیر مقدار خطای یک نمونه در شبکه عصبی را نشان می‌دهد:

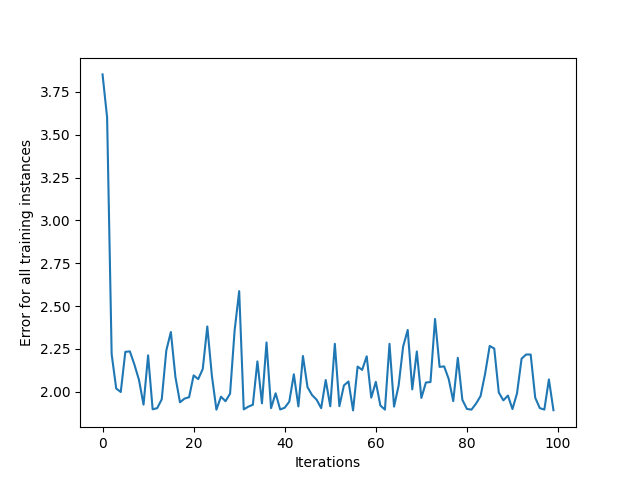
همان‌طور که می‌بینید، به طور کلی خطا در حال کاهش است. بعد از یک کاهش بزرگ در ابتدا، مقدار خطا به طور مداوم افزایش و کاهش پیدا می‌کند. دلیل این اتفاق تصادفی و کوچک بودن دیتاست است که باعث شده شبکه عصبی کار سختی پیش رو داشته باشد.

اما ارزیابی عملکرد بر اساس این شاخص کار درستی نیست چرا که شما شبکه عصبی را بر اساس داده‌هایی که از قبل دیده می‌سنجید. این کار منجر به بروز اتفاق بیش برازش (یا Overfitting) می‌شود که در آن مدل آن‌قدر خوب با دیتاست آموزشی خوب کار می‌کند که نمی‌تواند آن را به داده‌های دیگر تعمیم دهد.

ساخت هوش مصنوعی ساده با پایتون: قسمت اول، مفاهیم و اصول اولیه شبکه‌های عصبی

اضافه کردن لایه‌های بیشتر

دیتاست این آموزش بسیار کوچک است. به طور معمول مدل‌های یادگیری عمیق به دلیل پیچیدگی دیتاست و وجود داده‌های اشتباه، از حجم بزرگی از داده بهره می‌برند. از آن‌جایی که این دیتاست‌ها بسیار بزرگ و پیچیده هستند، استفاده از یک یا دو لایه جوابگوی نیاز‌ها نیست. به همین دلیل روی واژه «عمیق» در یادگیری عمیق تاکید می‌کنیم.

با اضافه کردن لایه‌های بیشتر قدرت پردازش شبکه عصبی نیز بیشتر شده و قادر به انجام پیش‌بینی‌های سطح بالا است. یکی از انواع این پیش‌بینی‌ها تشخیص چهره است که در آن شبکه عصبی تصویر شما را با تصویر موجود در دیتاست مقایسه کرده و نقاط مشترک را تشخیص می‌دهد.

سرویس تشخیص چهره پادیوم با اتکاء بر همین فناوری آماده ارائه به کسب‌وکارهای متقاضی است. فقط کافی است فرم زیر را پر کنید تا کارشناسان ما در اولین فرصت با شما تماس بگیرند: